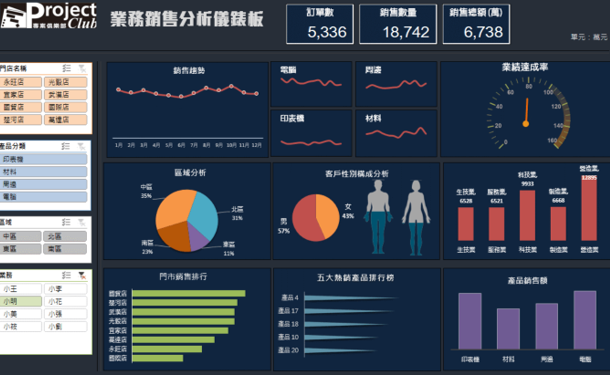
許多人因為工作需求要學習數據分析,進而接觸統計學名詞,像是迴歸分析(英語:Regression Analysis),是一個使用線性模型函數預測數據的方法,透過無線多條線找出點到線平均最短的距離,而那條平均線即為線性迴歸。
迴歸分析目的在於了解兩個或多個變數之間是否存在正負相關與強度,並建立數學模型以便我們預測在只有一個自變數變化時應變數的變化量。

在學習統計學的路上,是否曾經看過類似對於迴歸分析名詞的解釋,使你不斷地重複咀嚼著,依舊難以理解,因此就陷進了「知識的詛咒」(The Curse of Knowledge)呢?本篇文章將帶你破解書中知識的詛咒!將迴歸分析化繁為簡,一步步地帶著你操作。
化繁為簡,回歸平凡

達爾文表弟法蘭西斯.高爾頓(Francis Galton)認為:
應該將達爾文的進化論應用在人類的進化上,因此他嘗試分析其中的關係,
假設父母身高很高,孩子的身高也會很高,而且高個子的人更喜歡和高個子的人結婚;
相反地,如果父母身高低孩子的身高變低,因此矮個子的人更喜歡跟矮個子二人結婚。
如果按照這種假設
人類不斷地發展會變成高個子跟矮個子兩個極端組合,然而多年過去了,這種身高兩極化並沒有發生,
因此從身高這麼簡單的數據來看支配人類的法則也存在許多誤差以及分散,於是就產生了「身高更接近平均值而不是理論預測」
回歸平凡
高爾頓稱之為「回歸平凡」,針對這種迴歸平均值現象的分析方法統計學則稱之為「均值回歸」(MEAN REVERSION),即所謂的迴歸分析!
上述故事讓我們理解到迴歸分析是透過觀察未來的趨勢發展變化,彼此之間的變數會朝什麼方向前進,進而找出變數間的相互關係後,使我們可以更能推測出未來的變化。
迴歸分析並不難,第一次操作就上手!
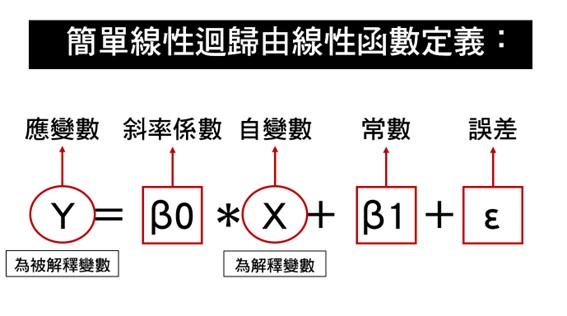
在進行迴歸分析前,需要了解什麼是自變數(independent variable)什麼是應變數(dependent variable),
ex:濕度多寡會影響發霉的程度,濕度就是自變數,而會被濕度影響的發霉就是應變數。
假設
如果今天要查看廣告投放的頻率越多,顧客的購買意願是否會增加,
問題即為廣告頻率(自變數)與購買數量(應變數)兩者的關係,以下帶著大家進行Excel迴歸分析的實際操作。
迴歸分析實作步驟1-3
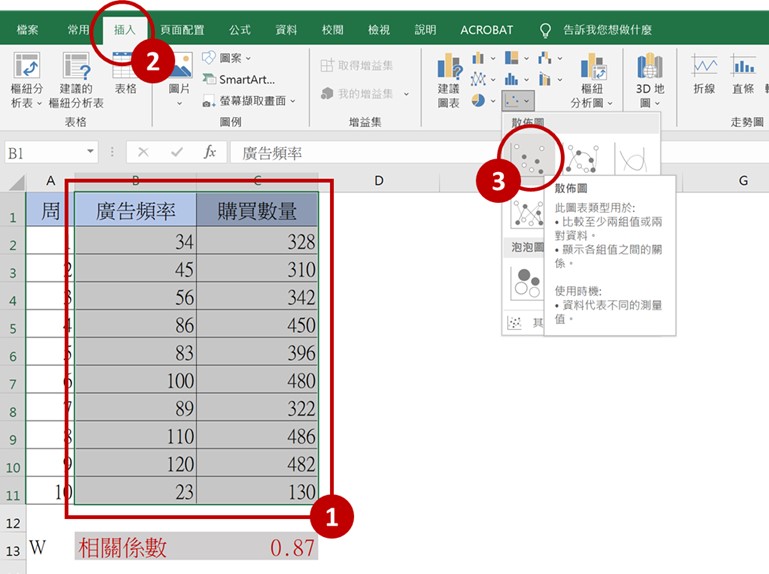
Step1~3 使用游標圈選廣告頻率與購買數量兩種變數(如圖 1紅框),接著點擊上方標籤的插入,並找到圖表區點選散佈圖。
迴歸分析實作步驟4-5
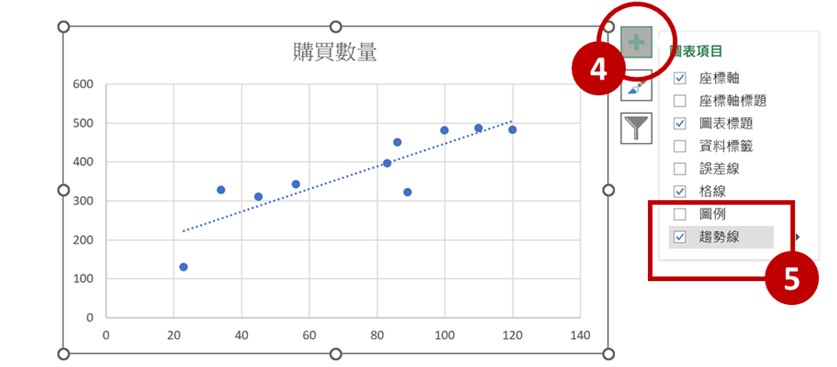
Step4~5游標點擊圖表右上的+號鍵,再點擊趨勢線,此趨勢線即為線性回歸
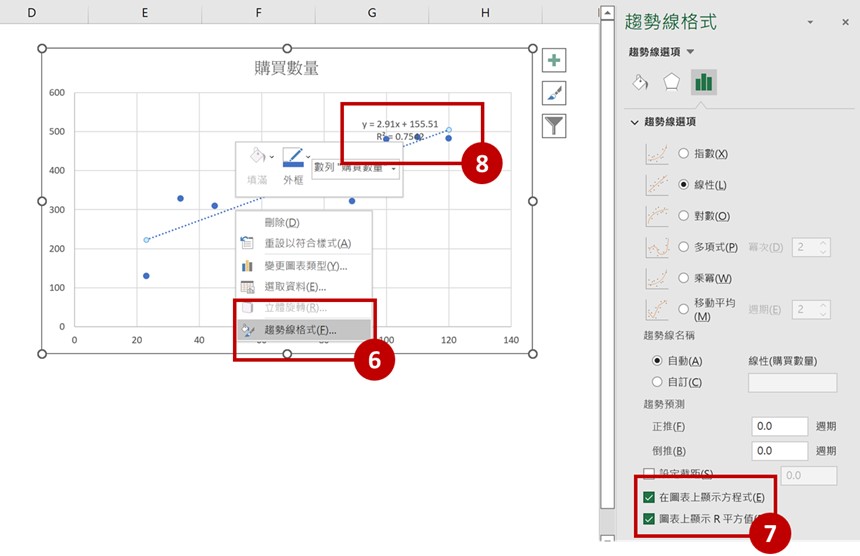
Step6~8對著趨勢線按右鍵,選取趨勢線格式,勾選「在圖表顯示方程式」即會出現迴歸的線性方程式;
勾選「圖表上顯示R平方值」即會出現數據的偏離程度。
據方程式斜率我們可以知道,廣告每播一次就會有2.91個人會進行購買,而常數是指廣告一曝光,就會有155.51的人會進行購買。
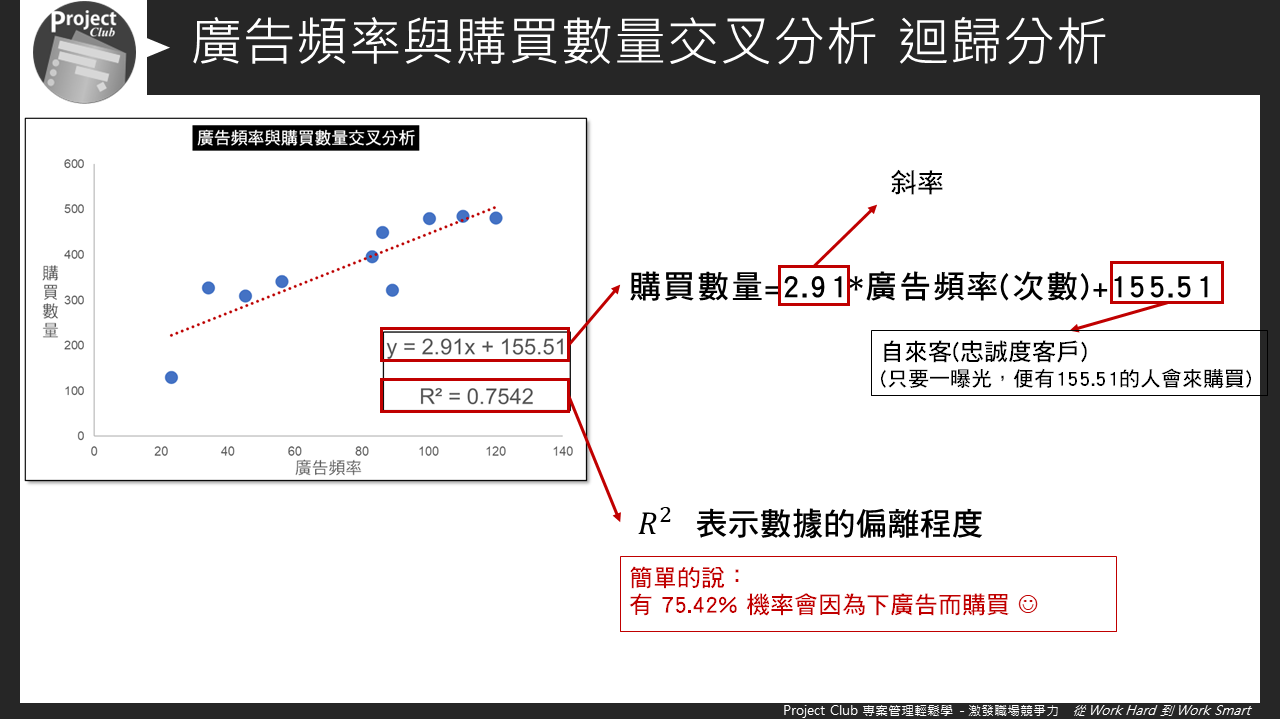
R平方就是計算機率有多高,簡單的說就是指75.42%機率會因為下廣告而購買,
透過簡單的理解,我們可以知道迴歸分析真的並不複雜!
下次進行迴歸分析時再也不會陷入知識的詛咒裡!
如果你也想具備數據分析的能力,絕對不能錯過這堂直播課程!也可以避掉一些數據分析的地雷和迷失!
Project Club 責任編輯:辜靖雯/Wendy

作者:游振昌
●專案管理顧問有限公司 執行長
●中華國際專案經理人協會 理事長
●Project Club 發起人暨資深顧問